Restricting Presolve Reductions
 PREVIOUS
NEXT
PREVIOUS
NEXT
| > Advanced Programming Techniques > Advanced Presolve Routines > Restricting Presolve Reductions |
Restricting Presolve Reductions |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
As mentioned in Introduction to Presolve, some presolve reductions are invalidated when a problem is modified. The advanced presolve interface therefore allows a user to tell presolve what sort of modifications will be made in the future, so presolve can avoid possibly invalid reductions. These considerations only apply to linear programs. Any modifications of QP or QCP models will cause ILOG CPLEX to discard the presolved model.
Consider adding a constraint to a problem after solving it. Imagine that you want to optimize a linear program:
Primal: |
Dual: | |||||||||||||||
max |
-x1 |
+ |
x2 |
+ |
x3 |
min |
6y1 |
+ |
5y2 | |||||||
st |
x1 |
+ |
x2 |
+ |
2x3 |  |
6 |
st |
y1 | 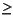 |
-1 | |||||
x2 |
+ |
x3 |  |
5 |
y1 |
+ |
y2 | 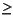 |
1 | |||||||
0 |
2y1 |
+ |
y2 | 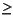 |
1 | |||||||||||
x1, |
x2, |
x3 | 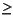 |
0 |
y1, |
y2, |
y3 | 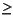 |
0 | |||||||
Note that the first constraint in the dual (y1 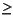 -1) is redundant. Presolve can use this information about the dual problem (and complementary slackness) to conclude that variable x1 can be fixed to 0 and removed from the presolved problem. While it may be intuitively obvious from inspection of the primal problem that x1 can be fixed to 0, it is important to note that dual information (redundancy of the first dual constraint) is used to formally prove it.
-1) is redundant. Presolve can use this information about the dual problem (and complementary slackness) to conclude that variable x1 can be fixed to 0 and removed from the presolved problem. While it may be intuitively obvious from inspection of the primal problem that x1 can be fixed to 0, it is important to note that dual information (redundancy of the first dual constraint) is used to formally prove it.
Now consider the addition of a new constraint x2  5x1:
5x1:
Primal: |
Dual: | |||||||||||||||
max |
-x1 |
+ |
x2 |
+ |
x3 |
min |
6y1 |
+ |
5y2 | |||||||
st |
x1 |
+ |
x2 |
+ |
2x3 |  |
6 |
st |
y1 |
- |
5y3 | 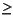 |
-1 | |||
x2 |
+ |
x3 |  |
5 |
y1 |
+ |
y2 |
+ |
y3 | 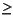 |
1 | |||||
- 5x1 |
+ |
x2 |  |
0 |
2y1 |
+ |
y2 | 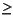 |
1 | |||||||
x1, |
x2, |
x3 | 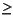 |
0 |
y1, |
y2, |
y3 | 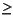 |
0 | |||||||
Our goal is to add the appropriate constraint to the presolved problem and reoptimize. Note, however, that the dual information presolve used to fix x1 to 0 was changed by the addition of the new constraint. The first constraint in the dual is no longer guaranteed to be redundant, so the original fixing is no longer valid (the optimal solution is now x1=1, x2=5, x3=0). As a result, CPLEX is unable to use the presolved problem to reoptimize.
We classify presolve reductions into several classes: those that rely on primal information, those that rely on dual information, and those that rely on both. Future addition of new constraints, modifications to objective coefficients, and tightening of variable bounds (a special class of adding new constraints) require the user to turn off dual reductions. Introduction of new columns, modifications to right-hand-side values, and relaxation of variable bounds (a special case of modifying right-hand-side values) require the user to turn off primal reductions.
These reductions are controlled through the CPX_PARAM_REDUCE parameter. The parameter has four possible settings. The default value CPX_PREREDUCE_PRIMALANDDUAL (3) indicates that presolve can rely on primal and dual information. With setting CPX_PREREDUCE_DUALONLY (2), presolve only uses dual information, with setting CPX_PREREDUCE_PRIMALONLY (1) it only uses primal information, and with setting CPX_PREREDUCE_NO_PRIMALORDUAL (0) it uses neither (which is equivalent to turning presolve off).
Setting the CPX_PARAM_REDUCE parameter has one additional effect on the optimization. Normally, the presolved problem and the presolved solution are freed at the end of an optimization call. However, when CPX_PARAM_REDUCE is set to a value other than its default, CPLEX assumes that the problem will subsequently be modified and reoptimized. It therefore retains the presolved problem and any presolved solution information (internally to the LP problem object). If the user has set CPX_PARAM_REDUCE and is finished with problem modification, the user can call CPXfreepresolve to free the presolved problem and reclaim the associated memory. The presolved problem is automatically freed when the user calls CPXfreeprob on the original problem.
We should note that cutting planes in mixed integer programming are handled somewhat differently than one might expect. If a user wishes to add his own cuts during the branch & cut process (through CPXaddusercuts or CPXcutcallbackadd), it may appear necessary to turn off dual reductions to accommodate them. However, for reasons that are complex and beyond the scope of this discussion, dual reductions can be left on. The reasons relate to the fact that valid cuts never exclude integer feasible solutions, so dual reductions performed for the original problem are still valid after cutting planes are applied. However, a small set of reductions does need to be turned off. Recall that presolve must translate a new constraint on the original problem into a constraint on variables in the presolved problem. Most reductions performed by CPLEX presolve replace variables with linear expressions of zero or more other variables (plus a constant). A few do not. These latter reductions make it impossible to perform the translation to the presolved problem. Set CPX_PARAM_PRELINEAR to 0 to forbid these latter reductions.
Restricting the type of presolve reductions will also allow presolve to conclude more about infeasible and/or unbounded problems. Under the default setting of CPX_PARAM_REDUCE, presolve can only conclude that a problem is infeasible and/or unbounded. If CPX_PARAM_REDUCE is set to CPX_PREREDUCE_PRIMALONLY (1), presolve can conclude that a problem is primal infeasible with return status CPXERR_PRESLV_INF. If CPX_PARAM_REDUCE is set to CPX_PREREDUCE_DUALONLY (2), presolve can conclude that a problem is primal unbounded (if it is primal feasible) with return status CPXERR_PRESLV_UNBD.
| Reminder |
| The previous paragraph applies to CPXpresolve, not CPXlpopt. |
A final facility that modifies the set of reductions performed by presolve is the CPXcopyprotected routine. The user provides as input a list of variables in the original problem that should survive presolve (that is, should exist in the presolved problem). Presolve will avoid reductions that remove those variables, with one exception. If a protected variable can be fixed, presolve will still remove it from the problem. This command is useful in cases where the user wants to explicitly control some aspect of the branch & cut process (for example, through the branch callback) using knowledge about those variables.
| Copyright © 1987-2003 ILOG, S.A. All rights reserved. Legal terms. | PREVIOUS NEXT |