All the building blocks are now in place to implement a method that creates a model. The diet problem consists of finding the least expensive diet using a set of foods such that all nutritional requirements are satisfied. The example in this chapter builds the specific diet model, chooses an optimizing algorithm, and shows how to access more detailed information about the solution.

The example includes a set of foods, where food j has a unit cost of foodCost[j]. The minimum and maximum amount of food j which can be used in the diet is designated foodMin[j] and foodMax[j], respectively. Each food j also has a nutritional value nutrPerFood[i][j] for all possible nutrients i. The nutritional requirement states that in the diet the amount of every nutrient i consumed must be within the bounds nutrMin[i] and nutrMax[i].

Mathematically, this problem can be modeled using a variable Buy[j] for each food j indicating the amount of food j to buy for the diet. Then the objective is:

minimize 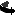_j (Buy[j] * foodCost[j])

The nutritional requirements mean that the following conditions must be observed; that is, for all i:

nutriMin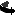[i] i nutrPerFood[i][j] * Buy[j] nutriMax[i]

Finally, every food must be within its bounds; that is, for all j:

foodMin[j] Buy[j] foodMax[j]

With what you have learned so far, you can implement a method that creates such a model.

  static void buildModelByRow(IloModeler    model,
                              Data          data,
                              IloNumVar[]   Buy,
                              IloNumVarType type) 
                                               throws IloException {
    int nFoods = data.nFoods;
    int nNutrs = data.nNutrs;

    for (int j = 0; j < nFoods; j++) {
      Buy[j] = model.numVar(data.foodMin[j], data.foodMax[j], type);
    }
    model.addMinimize(model.scalProd(data.foodCost, Buy));

    for (int i = 0; i < nNutrs; i++) {
      model.addRange(data.nutrMin[i],
                     model.scalProd(data.nutrPerFood[i], Buy),
                     data.nutrMax[i]);
    }
  }

The function receives several parameters. The parameter model is used for two things:

The argument data contains the data for the model to be built. The argument Buy is an array, initialized to length data.nFoods, containing the model's variables. Finally, parameter type is used to specify the type of the variables being created.

The function starts by creating the modeling variables, one by one, and storing them in array Buy. Each variable j is initialized to have bounds data.foodMin[j] and data.foodMax[j] and to be of type type.

The variables are first used to construct the objective function expression with method model.scalProd(foodCost, Buy). This expression is immediately used to create the minimization objective which is directly added to the active model by addMinimize.

In the loop that follows, the nutritional constraints are added. For each nutrient i the expression representing the amount of nutrient in a diet with food levels Buy is computed using model.scalProd(nutrPerFood[i], Buy). This amount of nutrient must be within the ranged constraint bounds nutrMin[i] and nutrMax[i]. This constraint is created and added to the active model with addRange.

Note that function buildModelByRow uses interface IloModeler rather than IloCplex. This allows the function to be called without change in another implementation of IloModeler, such as IloSolver.