Previous sections focused on how to diagnose the causes of infeasibility. However, you may want to go beyond diagnosis to perform automatic correction of your model and then proceed with delivering a solution. One approach for doing so is to build your model with explicit slack variables and other modeling constructs, so that an infeasible outcome is never a possibility. Such techniques for formulating a model are beyond the scope of this discussion, but you should consider them if you want the greatest possible flexibility in your application.

FeasOpt accepts an infeasible model and selectively relaxes the bounds and constraints in a way that minimizes a weighted penalty function that you define. In essence, FeasOpt tries to suggest the least change that would achieve feasibility. FeasOpt does not actually modify your model. Instead, it returns a suggested set of bounds and constraint ranges, along with the solution that would result from these relaxations. Your application can report these values directly, or it can apply these new values to your model, or you can run FeasOpt again with different weights perhaps to find a more acceptable relaxation.

In the various Concert Technology APIs, you have a choice of three versions of FeasOpt, specifying that you want to allow changes to the bounds on variables, to the ranges on constraints, or to both. In the Callable Library, only the last of these calling sequences is available. In each of the APIs, there is an additional argument where you specify whether you want merely a feasible solution suggested by the bounds and ranges that FeasOpt identifies, or an optimized solution that uses these bounds and ranges.

You specify the bounds or ranges that FeasOpt may consider for modification, by assigning positive preference values for each. A negative or zero preference means that the associated bound or range is not to be modified. The weighted penalty function is constructed from these preferences, like this: 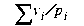where v_i is the violation and p_i is the preference.

Thus, the larger the preference, the more likely it will be that a given bound or range will be modified. However, it is not necessary to specify a unique preference for each bound or range. In fact, it is conventional to use only the values 0 (zero) and 1 (one) except when your knowledge of the problem suggests assigning explicit preferences.

The following examples show you how to use FeasOpt. These fragments of code are written in Concert Technology for C++ users, but the same principles apply to the other APIs as well. The examples begin with a model similar to one that you have seen repeatedly in this manual.

      IloEnv   env;
      IloModel model(env);
      IloNumVarArray x(env);
      IloRangeArray con(env);
      IloNumArray vals(env);

      x.add(IloNumVar(env, 0.0, 40.0));
      x.add(IloNumVar(env));
      x.add(IloNumVar(env));

      model.add(IloMaximize(env, x[0] + 2 * x[1] + 3 * x[2]));
      con.add( - x[0] +     x[1] + x[2] <=  20);
      con.add(   x[0] - 3 * x[1] + x[2] <=  30);
      con.add(   x[0] +     x[1] + x[2] >= 150);
      model.add(con);

If you extract that model and solve it, by means of the following lines, you find that it is infeasible.

 IloCplex cplex(model);
 cplex.solve();
 if ( cplex.getStatus() == IloAlgorithm::Infeasible ||
      cplex.getStatus() == IloAlgorithm::InfeasibleOrUnbounded ) {
      env.out() << endl << "*** Model is infeasible ***" << endl << endl;

Now the following lines invoke FeasOpt to locate a feasible solution:

// begin feasOpt analysis

cplex.setOut(env.getNullStream());
IloNumArray lb(env);
IloNumArray ub(env);

// first feasOpt call

env.out() << endl << "*** First feasOpt call ***" << endl;
env.out() << "*** Consider all constraints ***" << endl;
int rows = con.getSize();
lb.add(rows, 1.0);
ub.add(rows, 1.0);

if ( cplex.feasOpt(con, lb, ub, IloTrue) ) {
    env.out() << endl;
    env.out() << "*** Suggested lower range = " << lb << endl;
    env.out() << "*** Suggested upper range = " << ub << endl;
    env.out() << "*** Feasible objective value would be = "
                               << cplex.getObjValue() << endl;
    env.out() << "Solution status    = " << cplex.getStatus() << endl;
    env.out() << "Solution obj value = " << cplex.getObjValue() << endl
           env.out() << "Values             = " << vals << endl;
           env.out() << endl;
    }
    else {
        env.out() << "*** Could not repair the infeasibility" << endl;
        throw (-1);
      }

The code first turns off logging to the screen by the optimizers, simply to avoid unnecessary output. It then allocates arrays lb and ub, to contain the preferences as input, and to receive the modified constraint ranges as output. The preference is set to 1.0 for all three constraints in both directions to indicate that any change to a constraint range will be permissible.

Then FeasOpt is called, with the setting of IloTrue for the argument that specifies whether to return an optimized solution. If the FeasOpt call succeeds, then several lines of output give the results. Here is the output:

*** First feasOpt call ***
*** Consider all constraints ***

*** Suggested lower range = [-INF, -INF, 150]
*** Suggested upper range = [70, 30, INF]
*** Feasible objective value would be = 340
Solution status    = Infeasible
Solution obj value = 340
Values             = [40, 30, 80]

There are several items of note in this output. First, you see that FeasOpt recommends only the first constraint to be modified, namely, by changing the constraint from its original form:

- x[0] +     x[1] + x[2] <=  20

to the following:

- x[0] +     x[1] + x[2] <=  70

The solution values of [40, 30, 80] would be feasible in the modified version of the constraint, but not in the original version. This situation is reflected by the fact that the solution status has not changed from its value of Infeasible. In other words, this change to the right-hand side (RHS) of the constraint is only a suggestion from FeasOpt; the model itself has not changed, and the proposed solution is still infeasible in it.

To get a more concrete idea, assume that this constraint represents a limit on a supply, and assume further that increasing the supply to 70 is not practical. Now rerun FeasOpt, not allowing this constraint to be modified, like this:

// second feasOpt call

env.out() << endl << "*** Second feasOpt call ***" << endl;
env.out() << "*** Consider all but first constraint ***" << endl;

// re-set all indicator variables because they now contain values
lb[0]=ub[0]=0.0;
lb[1]=ub[1]=1.0;
lb[2]=ub[2]=1.0;

if ( cplex.feasOpt(con, lb, ub, IloTrue) ) {
     env.out() << endl;
     env.out() << "*** Suggested lower range = " << lb << endl;
     env.out() << "*** Suggested upper range = " << ub << endl;
     env.out() << "*** Feasible objective value would be = "
                                  << cplex.getObjValue() << endl;
     env.out() << "Solution status    = " << cplex.getStatus() << endl;
     env.out() << "Solution obj value = " << cplex.getObjValue() << endl;
     cplex.getValues(vals, x);
     env.out() << "Values             = " << vals << endl; 
     env.out() << endl;
    }
    else {
         env.out() << "*** Could not repair the infeasibility" << endl;
         throw (-1);
}

In those lines, preferences about the lower and upper bounds, in the arrays lb and ub, were set because they contained the results from the first FeasOpt call. Also those lines disallow any changes to the first constraint by setting lb[0]=ub[0]=0.0. FeasOpt runs again, and here are the results of this second run:

*** Second feasOpt call ***
*** Consider all but first constraint ***
*** Suggested lower range = [-INF, -INF, 100]
*** Suggested upper range = [20, 30, INF]
*** Feasible objective value would be = 202.5
Solution status    = Infeasible
Solution obj value = 202.5
Values             = [40, 17.5, 42.5]

Notice that the projected maximal objective value is quite different from the first time, as are the optimal values of the three variables. This solution was completely unaffected by the previous call to FeasOpt. This solution also is infeasible with respect to the original model, as you would expect. (If it had been feasible, you would not have needed FeasOpt in the first place.)

That second call changed the range of a constraint. Now consider changes to the bounds.

// third feasOpt call

env.out() << endl << "*** Third feasOpt call ***" << endl;
env.out() << "*** Consider all bounds ***" << endl;

// re-use indicator variables - they happen to be right dimension
lb[0]=ub[0]=1.0;
lb[1]=ub[1]=1.0;
lb[2]=ub[2]=1.0;

if ( cplex.feasOpt(x, lb, ub, IloTrue) ) {
    env.out() << endl;
    env.out() << "*** Suggested lower bounds = " << lb << endl;
    env.out() << "*** Suggested upper bounds = " << ub << endl;
    env.out() << "*** Feasible objective value would be = "
                                   << cplex.getObjValue() << endl;
        env.out() << "Solution status    = " << cplex.getStatus() << endl;
    env.out() << "Solution obj value = " << cplex.getObjValue()<< endl;
    cplex.getValues(vals, x);
    env.out() << "Values             = " << vals << endl;
    env.out() << endl;
   }
   else {
        env.out() << "*** Could not repair the infeasibility" << endl;
        throw (-1);
}

In those lines, all six bounds (lower and upper bounds of three variables) are considered for possible modification because a preference of 1.0 is set for each of them. Here is the result:

*** Third feasOpt call ***
*** Consider all bounds ***

*** Suggested lower bounds = [0, 0, 0]
*** Suggested upper bounds = [65, 1e+20, 1e+20]
*** Feasible objective value would be = 290
Solution status    = Infeasible
Solution obj value = 290
Values             = [65, 30, 55]

Those results suggest modifying only one bound, the upper bound on the first variable. (The value 1e+20 serves as Infinity on the variables having no upper bound.) And just as you might expect, the solution value for that first variable is exactly at its upper bound; there is no incentive in the weighted penalty function to set the bound any higher than it has to be to achieve feasibility.

Now assume for some reason it is undesirable to let this variable have its bound modified. The final call to FeasOpt changes the preference to achieve this effect, like this:

// fourth feasOpt call

env.out() << endl << "*** Fourth feasOpt call ***" << endl;
env.out() << "*** Consider all bounds except first ***" << endl;
lb[0]=ub[0]=0.0;
lb[1]=ub[1]=1.0;
lb[2]=ub[2]=1.0;

if ( cplex.feasOpt(x, lb, ub, IloTrue) ) {
    env.out() << endl;
    env.out() << "*** Suggested lower bounds = " << lb << endl;
    env.out() << "*** Suggested upper bounds = " << ub << endl;
    env.out() << "*** Feasible objective value would be = "
                                   << cplex.getObjValue() << endl;
    env.out() << "Solution status    = " << cplex.getStatus() << endl;
    env.out() << "Solution obj value = " << cplex.getObjValue() << endl;
    cplex.getValues(vals, x);
    env.out() << "Values             = " << vals << endl;
    env.out() << endl;
   }
    else {
        env.out() << "*** Could not repair the infeasibility" << endl;
        throw (-1);
}

Then after the fourth call of FeasOpt, the output to the screen looks like this:

*** Fourth feasOpt call ***
*** Consider all bounds except first ***
*** Could not repair the infeasibility
Unknown exception caught

This is a correct outcome, and a more nearly complete application should catch this exception and handle it appropriately. FeasOpt is telling the user here that no modification to the model is possible under this set of preferences: only the bounds on the last two variables are permitted to change according to the preferences expressed by the user, and they are already at [0,+inf], so the upper bound can not increase, and no negative value for the lower bounds would ever improve the feasibility of this model. Not every infeasibility can be repaired, and an application calling FeasOpt will usually need to take this possibility into account.