Stating a MIP Problem

> Discrete Optimization > Solving Mixed Integer Programming Problems (MIP) > Stating a MIP Problem

Stating a MIP Problem

A mixed integer programming (MIP) problem may contain both integer and continuous variables. If the problem contains an objective function with no quadratic term, (a linear objective), then the problem is termed a Mixed Integer Linear Program (MILP). If there is a quadratic term in the objective function, the problem is termed a Mixed Integer Quadratic Program (MIQP). If the model has any constraints containing a quadratic term, regardless of the objective function, the problem is termed a Mixed Integer Quadratically Constrained Program (MIQCP).

In ILOG CPLEX documentation, if the discussion pertains specifically to either the MILP or MIQP case, then that term is used. For the majority of topics that pertain equally to MILP, MIQP, and MIQCP, the comprehensive term MIP is used.

Integer variables may be restricted to the values 0 (zero) and 1 (one), in which case they are referred to as binary variables. Or they may take on any integer values, in which case they are referred to as general integer variables. A variable of any MIP that may take either the value 0 (zero) or a value between a lower and an upper bound is referred to as semi-continuous. A semi-continuous variable that is restricted to integer values is referred to as semi-integer. Using Semi-Continuous Variables says a bit more about semi-continuous variables later in this chapter. Special Ordered Sets (SOS) are discussed in Using Special Ordered Sets. Continuous variables in a MIP problem are those which are not restricted in any of these ways, and are thus permitted to take any solution value within their (possibly infinite) lower and upper bounds.

In ILOG CPLEX documentation, the comprehensive term integer variable means any of the various types just mentioned except for continuous or SOS. The presence or absence of a quadratic term in the objective function or among the constraints for a given variable has no bearing on its being classified as continuous or integer.

The following illustrates a mixed integer programming problem, which is solved in the example program ilomipex1.cpp / mipex1.c, discussed later in this chapter:

Maximize		x1	+	2x2	+	3x3	+	x4
subject to	-	x1	+	x2	+	x3	+	10x4		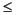20
		x1	-	3x2	+	x3		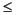		30
				x2			-	3.5x4	=	0
with these bounds		0		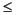x1		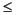40
		0		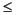x2		+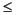
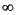		0		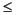x3		+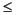
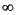		2		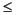x4		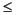3
				x4	integer

PREVIOUS NEXT