Identifying a Quadratically Constrained Program (QCP)
 PREVIOUS
NEXT
PREVIOUS
NEXT
| > Continuous Optimization > Solving Problems with Quadratic Constraints (QCP) > Identifying a Quadratically Constrained Program (QCP) |
Identifying a Quadratically Constrained Program (QCP) |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
The distinguishing characteristic of QCP is that quadratic terms may appear in one or more constraints of the problem. The objective function of such a problem may or may not contain quadratic terms as well. Thus, the most general formulation of a QCP is:
Minimize 1/2 xTQx + cTx
subject to Ax ~ b
and aiTx + xTQix  ri for i=1,...,q
ri for i=1,...,q
with these bounds l  x
x  u
u
As with a quadratic objective function, convexity plays an important role in quadratic constraints. The constraints must each define a convex region. To make sure of convexity, ILOG CPLEX requires that each Qi matrix be positive semi-definite (PSD). The following sections offer more information about these concepts.
The inequality x2 + y2  1 is convex. To give you an intuitive idea about convexity, Figure 12.1 graphs that inequality and shades the area that it defines as a constraint. If you consider a and b as arbitrary values in the domain of the constraint, you see that any continuous line segment between them is contained entirely in the domain.
1 is convex. To give you an intuitive idea about convexity, Figure 12.1 graphs that inequality and shades the area that it defines as a constraint. If you consider a and b as arbitrary values in the domain of the constraint, you see that any continuous line segment between them is contained entirely in the domain.
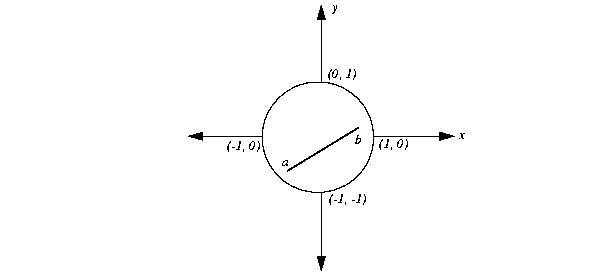
 1 is convex
1 is convex
The inequality x2 + y2 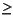 1 is not convex; it is concave. Figure 12.2 graphs that inequality and shades the area that it defines as a constraint. If you consider c and d as arbitrary values in the domain of this constraint, then you see that there may be continuous line segments that join the two values in the domain but pass outside the domain of the constraint to do so.
1 is not convex; it is concave. Figure 12.2 graphs that inequality and shades the area that it defines as a constraint. If you consider c and d as arbitrary values in the domain of this constraint, then you see that there may be continuous line segments that join the two values in the domain but pass outside the domain of the constraint to do so.
 1 is not convex
1 is not convex
It might be less obvious at first glance that the equality x2 + y2 = 1 is not convex either. As you see in Figure 12.3, there may be a continuous line segment that joins two arbitrary points, such as e and f, in the domain but the line segment may pass outside the domain. Another way to see this idea is to note that an equality constraint is algebraically equivalent to the intersection of two inequality constraints of opposite sense, and you have already seen that at least one of those quadratic inequalities will not be convex. Thus, the equality is not convex either.
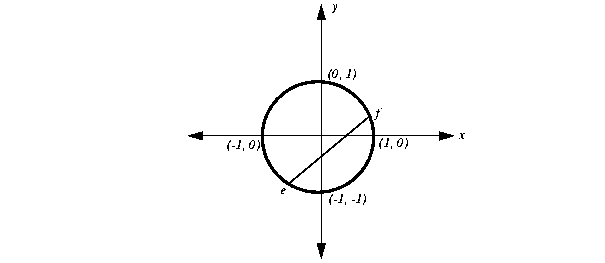
Identifying a Quadratically Constrained Program (QCP) explained that the quadratic matrix in each constraint must be positive semi-definite (PSD), thus providing convexity. A matrix Qi is PSD if xTQix 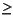 0 for every vector x, whether or not x is feasible. Other issues pertaining to positive semi-definiteness are discussed in the context of a quadratic objective function in Identifying Convex QPs.
0 for every vector x, whether or not x is feasible. Other issues pertaining to positive semi-definiteness are discussed in the context of a quadratic objective function in Identifying Convex QPs.
When you call the barrier optimizer, your quadratic constraints will be checked for the necessary PSD property, and an error status 5002 will be returned if any of them violate it.
There is one exception to the PSD requirement; that is, there is an additional form of quadratic constraint which is accepted but is not covered by the general formulation in Identifying a Quadratically Constrained Program (QCP). Technically, the quadratically constrained problem class that the barrier optimizer solves is a Second-Order Cone Program (SOCP). ILOG CPLEX, through its preprocessing feature, makes the translation to SOCP for you, transparently, returning the solution in terms of your original formulation. A constraint will be accepted for solution by the barrier optimizer if it can be transformed to the following convex cone constraint:
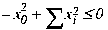
That formulation is distinguished primarily by the specific signs of the coefficients and by the lack of a linear term, where x0 is a nonnegative variable
| Copyright © 1987-2003 ILOG, S.A. All rights reserved. Legal terms. | PREVIOUS NEXT |