The cutting stock problem in this chapter is sometimes known in math programming terms as a knapsack problem with reduced cost in the objective function.

Generally, a cutting stock problem begins with a supply of rolls of material (the stock). Strips are cut from a continuous roll. All the strips cut from one roll are known together as a pattern. The point of this example is to use as few rolls of stock as possible to satisfy some specified demand. By convention, it is assumed that only one pattern is laid out across the stock; consequently, only one dimension - the width - of each roll of stock is important.

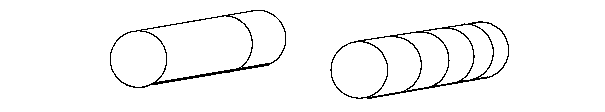
Even with that simplifying assumption, the fact that there can be so many different patterns makes a naive model of this problem (where a user declares one variable for every possible pattern) impractical. Such a model introduces too many symmetries. Fortunately, for any given customer order, a limited number of patterns will suffice, so many of the possible patterns can be disregarded, and the application can focus on finding the relevant ones.

Here is a conventional statement of a cutting stock problem in terms of the unknown Xj, the number of times that pattern j will be used, and Aij, the number of items i of each pattern j needed to satisfy demand di:

Minimize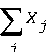

subject to 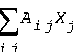with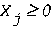

Solving this model with all columns present from the beginning is practically impossible. In fact, even with only 10 types of items with a size roughly 1/10 of the width of the roll, there would exist roughly 10^10 kinds of patterns, and hence that many decision variables. Such a formulation might not even fit in memory on a reasonably large computer. Moreover, most of those patterns would obviously not be interesting in a solution. These considerations make column generation an interesting approach for this problem.

To solve a cutting stock problem by column generation, start with a subproblem. Choose one pattern, lay it out on the stock, and cut as many items as possible, subject to the constraints of demand for that item and the width of the stock. This procedure will surely work in that it produces some answer (a feasible solution) to the problem, but it will not necessarily produce a satisfactory answer in this way.

To move closer to a satisfactory solution, the application can then generate other columns. That is, other decision variables (other Xj) will be chosen to add to the model. Those decision variables are chosen on the basis of their favorable reduced cost. In linear programming terms, choose variables for which the negative reduced cost improves the minimization. In this formulation of the rest of the problem, 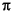_i represents the dual value of constraint i, like this:

Minimize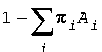

subject to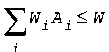

where W is the width of a roll of stock and Ai must be a nonnegative integer.