Some expressions are easily recognized as nonlinear, for example, a function such as x² + y² 1. However, other nonlinearities are less obvious, such as absolute value as a function. In a very real sense, MIP is a class of nonlinearly constrained problems because the integrality restriction destroys the property of convexity which the constraints otherwise might possess. Because of that characteristic, certain (although not all) nonlinearities are capable of being converted to a MIP formulation, and thus can be solved by ILOG CPLEX. In fact, IloCplex can extract the following nonlinear expressions in a C++ application:

For example, given these variables and arrays:

IloIntVarArray x(env, 5, 0, 1000);
IloNumVar y(env, -1000, 5000);
IloNumVar z(env, -1000, 1000);

IloCplex recognizes the following constraint as valid and extracts it:

IloMin(x) >= IloAbs(y)

In fact, ranges containing logical expressions can, in turn, appear in logical constraints. For example, the following constraint is valid and extractable by IloCplex:

IloIfThen(env, (IloAbs(y) <= 100), (z <= 300));

Linear constraints can appear as terms in logical constraints. A linear constraint appearing as a term in a logical constraint behaves like a binary value. For example, given x and y as variables, you can write the following lines to get the truth value of x 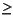y in a binary value:

IloIntVar b(env, 0, 1);
model.add(b == (x >= y));

Optimizing how many items appear in a solution is often an issue in practical problems. Questions of counting (how many?) can be represented formally as cardinality constraints. For example, suppose that your application includes three variables, each representing a quantity of one of three products, and assume further that a good solution to the problem means that the quantity of at least two of the three products must be greater than 20. Then you can represent that idea in your application, like this:

IloNumVarArray x(env, 3, 0, 1000);
model.add((x[0] >= 20) + (x[1] >= 20) + (x[2] >= 20) >= 2);

It is important to note here that only linear constraints can appear as arguments of logical constraints extracted by IloCplex. That is, quadratic constraints are not handled in logical constraints. Similarly, quadratic terms cannot appear as arguments of logical expressions such as IloMin, IloMax, IloAbs, and IloPiecewiseLinear.