What Is a Piecewise Linear Function?
 PREVIOUS
NEXT
PREVIOUS
NEXT
| > Discrete Optimization > Transport: Piecewise Linear Optimization > Piecewise Linearity in ILOG CPLEX > What Is a Piecewise Linear Function? |
What Is a Piecewise Linear Function? |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
From a geometric point of view, Figure 16.1 shows a conventional piecewise linear function f(x). This particular function consists of four segments. If you consider the function over four separate intervals, (-
, 4) and [4, 5) and [5, 7) and [7, 
), you see that f(x) is linear in each of those separate intervals. For that reason, it is said to be piecewise linear. Within each of those segments, the slope of the linear function is clearly increasing or decreasing. The points where the slope of the function changes are known as breakpoints. The piecewise linear function in Figure 16.1 has three breakpoints.
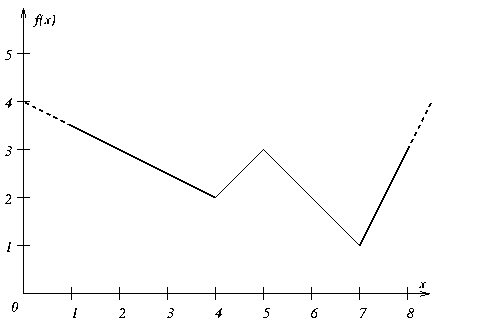
Piecewise linear functions are often used to represent or to approximate nonlinear unary functions (that is, nonlinear functions of one variable). For example, piecewise linear functions frequently represent situations where costs vary with respect to quantity or gains vary over time.
| Copyright © 1987-2003 ILOG, S.A. All rights reserved. Legal terms. | PREVIOUS NEXT |