What Does ILOG CPLEX Do?
 PREVIOUS
NEXT
PREVIOUS
NEXT
| > Meet ILOG CPLEX > What Does ILOG CPLEX Do? |
What Does ILOG CPLEX Do? |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
ILOG CPLEX is a tool for solving, first of all, linear optimization problems. Such problems are conventionally written like this:
Minimize (or maximize) |
c1x1 + c2x2 + . . . + cnxn | ||
subject to |
a11x1 + a12x2 + . . . + a1nxn |
~ |
b1 |
a21x1 + a22x2 + . . . + a2nxn |
~ |
b2 | |
. . . | |||
am1x1 + am2x2 + . . . + amnxn |
~ |
bm | |
with these bounds | 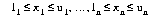 | ||
where the relation ~ may be greater than or equal to, less than or equal to, or simply equal to, and the upper bounds ui and lower bounds li may be positive infinity, negative infinity, or any real number.
When a linear optimization problem is stated in that conventional form, its coefficients and values are customarily referred to by these terms:
In the most basic linear optimization problem, the variables of the objective function are continuous in the mathematical sense, with no gaps between real values. To solve such linear programming problems, ILOG CPLEX implements optimizers based on the simplex algorithms (both primal and dual simplex) as well as primal-dual logarithmic barrier algorithms and a sifting algorithm. These alternatives are explained more fully in Chapter 8, Solving LPs: Simplex Optimizers.
ILOG CPLEX can also handle certain problems in which the objective function is not linear but quadratic. Such problems are known as quadratic programs or QPs. Chapter 11, Solving Problems with a Quadratic Objective (QP), covers those kinds of problems.
ILOG CPLEX also solves certain kinds of quadratically constrained problems. Such problems are known as quadratically constrained programs or QCPs. Chapter 12, Solving Problems with Quadratic Constraints (QCP), tells you more about the kinds of quadratically constrained problems that ILOG CPLEX solves.
ILOG CPLEX is also a tool for solving mathematical programming problems in which some or all of the variables must assume integer values in the solution. Such problems are known as mixed integer programs or MIPs because they may combine continuous and discrete (for example, integer) variables in the objective function and constraints. MIPs with linear objectives are referred to as mixed integer linear programs or MILPs, and MIPs with quadratic objective terms are referred to as mixed integer quadratic programs or MIQPs. Likewise, MIPs that are also quadratically constrained in the sense of QCP are known as mixed integer quadratically constrained programs or MIQCPs.
Within the category of mixed integer programs, there are two kinds of discrete integer variables: if the integer values of the discrete variables must be either 0 (zero) or 1 (one), then they are known as binary; if the integer values are not restricted in that way, they are known as general integer variables. This manual explains more about the mixed integer optimizer in Chapter 13, Solving Mixed Integer Programming Problems (MIP).
ILOG CPLEX also offers a Network Optimizer aimed at a special class of linear problem with network structures. ILOG CPLEX can optimize such problems as ordinary linear programs, but if ILOG CPLEX can extract all or part of the problem as a network, then it will apply its more efficient Network Optimizer to that part of your problem and use the partial solution it finds there to construct an advanced starting point to optimize the rest of the problem. Chapter 10, Solving Network-Flow Problems offers more detail about how the ILOG CPLEX Network Optimizer works.
| Copyright © 1987-2003 ILOG, S.A. All rights reserved. Legal terms. | PREVIOUS NEXT |