A network-flow problem finds the minimal-cost flow through a network, where a network consists of a set N of nodes and a set A of arcs connecting the nodes. An arc a in the set A is an ordered pair (i, j) where i and j are nodes in the set N; node i is called the tail or the from-node and node j is called the head or the to-node of the arc a. Not all the pairs of nodes in a set N are necessarily connected by arcs in the set A. More than one arc may connect a pair of nodes; in other words, a1 = (i, j) and a2 = (i, j) may be two different arcs in A, both connecting the nodes i and j in N.

Each arc a may be associated with four values:

Each node n is associated with one value:

By convention, a node with strictly positive supply value (that is, sn > 0) is called a supply node or a source, and a node with strictly negative supply value (that is, sn < 0) is called a demand node or a sink. A node where sn = 0 is called a transshipment node. The sum of all supplies must match the sum of all demands; if not, then the network flow problem is infeasible.

Tn is the set of arcs whose tails are node n; Hn is the set of arcs whose heads are node n. The usual form of a network problem looks like this:

Minimize (or maximize)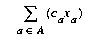

subject to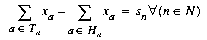

with these bounds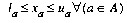

That is, for each node, the net flow entering and leaving the node must equal its supply value, and all flow values must be within their bounds. The solution of a network-flow problem is an assignment of flow values to arcs (that is, the modeling variables) to satisfy the problem formulation. A flow that satisfies the constraints and bounds is feasible.