Group optim.cplex.cpp

What is IloCplex?

IloCplex is a Concert Technology class derived from IloAlgorithm. Instances of this class are capable of solving optimization problems of the following types:

• Linear Programs (LPs),
• Mixed Integer Linear Programs (MILPs),
• Mixed Integer Programs (MIPs),
• Quadratic Programs (QPs),
• Mixed Integer Quadratic Programs (MIQPs),
• Quadratically Constrained Programs (QCPs);
• Mixed Integer Quadratically Constrained Programs (MIQCPs).

An instance of IloCplex can extract and solve models consisting of the following Concert Technology extractables:

What is special about this set of extractable classes recognized by IloCplex is that models consisting of these objects can be transformed into mathematical programming problems of the form:

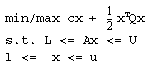
When all variables are continuous and Q is zero, problems of this form are known as Linear Programs (LPs). If Q is not zero, such problems are known as Quadratic Programs (QPs). If any variables are integer, semi-continuous, or Boolean, such problems are called Mixed Integer Programs (MIPs). A MIP with a zero Q matrix is called a Mixed Integer Linear Program (MILP), and a MIP with a non-zero Q is called a Mixed Integer Quadratic Program (MIQP). If there are quadratic constraints in the problem, and its variables are continuous, it is known as a Quadratically Constrained Program (QCP). If in addition to the quadratic constraints, there are discrete variables in the problem (such as integer, Boolean, or semi-continuous variables), then it is known as MIQCP.

• Objects of the class IloNumVar represent modeling variables. They are defined by the lower and upper bounds of the variable, and the type of the variable. The type of the variable can be one of these:
  • ILOFLOAT, for continuous,
  • ILOINT, for integer,
  • ILOBOOL, for Boolean variables.
• Objects of the class IloSemiContVar represent semi-continuous variables. A semi-continous variable may be 0 (zero) or may take a value within an interval defined by its semi-continuous lower and upper bounds. Semi-continuous variables are usually defined as continuous variables, but you can designate an instance of IloSemiContVar as integer by using the type indicator it inherits from IloNumVar.
• Objects of the class IloObjective represent objective functions of optimization models. IloCplex deals with models containing at most one objective function, and the objective function must be linear, piecewise linear, or quadratic.
• Objects of the class IloRange represent constraints of the form: lower bound ≤ expression ≤ upper bound. Any floating-point value or +/- IloInfinity can be used for the bounds.
• Objects of the class IloConversion change the type of a variable in a model. This class allows you to use the same variable with different types in different models.
• Objects of the class IloModel represent models which consist of extractable objects. They can be used to create submodels or additional models in a given environment.
• Objects of the class IloSOS1 represent type 1 Special Ordered Sets (SOSs). A type 1 SOS specifies that at most one variable from a set of variables may take a nonzero value. Similarly, objects of the class IloSOS2 represent type 2 SOSs. A type 2 SOS specifies that at most two variables from a set of variables may take nonzero values and that these two variables must be neighbors with respect to a specified order of the variables. SOS1 are rarely used and SOS2 are mostly used to model piecewise linear functions, for which Concert Technology provides direct support (with the class IloPiecewiseLinear).
• Objects of the class IloAnd are used in conjunction with objects of the class IloSolution.

Refer to the ILOG Concert Technology Reference Manual for more information about these classes.

IloCplex Optimizer Options

An instance of the class IloCplex is not really only one algorithm, but, in fact, consists of a set of highly configurable algorithms, also known as optimizer options. They include primal and dual simplex algorithms, barrier algorithm, a sifting algorithm, a network simplex algorithm, and a branch & cut algorithm for MIPs. Though in most cases IloCplex can be used like a black box, the optimizer options can be selected individually to provide a wealth of parameters that allow you to fine tune the algorithm to your particular model. In the case of the mixed integer optimizer, you can use your own goals or callbacks and directly control the branch & cut search carried out by IloCplex.

The most general kind of problem is a MIP. You might think of the LPs as a subset of MIPs: an LP is a problem in which the model is:

• without integer variables,
• without Boolean variables,
• without semi-continuous variables,
• without piecewise linear functions,
• without a quadratic component in the objective function,
• without quadratic constraints,
• and without a special ordered set (SOS).

For linear programming problems (LPs), a variety of additional solution information can be queried. These queries include dual information or, with the appropriate optimizer option, basis information. Sensitivity analysis allows you to analyze how you can modify your model while preserving the same solution. Or, if your model is infeasible, the infeasibility finder enables you to analyze the source of the infeasibility.